BAB V VEKTOR PADA BIDANG

        VEKTOR PADA BIDANG

Bentuk Komponen Suatu Vektor

Banyak kuantitas dalam geometri dan fisika, seperti luas, volume, suhu, massa, dan waktu, dapat dikarakteristikkan sebagai suatu bilangan real tunggal yang diskalakan terhadap satuan ukuran yang tepat. Kuantitas-kuantitas tersebut dinamakan kuantitas skalar, dan bilangan real yang berasosiasi dengan kuantitas tersebut dinamakan skalar.

Kuantitas-kuantitas lain, seperti gaya, kecepatan, dan percepatan, melibatkan nilai dan arah dan tidak dapat dikarakteristikkan hanya dengan suatu bilangan real tunggal. Ruas garis berarah digunakan untuk merepresentasikan kuantitas semacam itu, seperti yang ditunjukkan pada Gambar 1. Ruas garis berarah PQ memiliki titik pangkal P dan titik ujung Q, dan panjangnya (atau besarnya) dinotasikan sebagai ||PQ||. Ruas-ruas garis berarah yang memiliki panjang dan arah sama dikatakan ekuivalen, seperti yang ditunjukkan Gambar 2. Himpunan semua ruas garis berarah yang ekuivalen dengan ruas garis yang diberikan, PQ, merupakan suatu vektor pada bidang dan dinotasikan sebagai

Dalam pengetikan, vektor biasanya ditulis dalam huruf kecil dan tebal seperti u, v, dan w. Ketika ditulis tangan, vektor biasanya ditulis sebagai huruf kecil dengan tanda panah di atasnya.
Pastikan kita memahami bahwa suatu vektor merepresentasikan himpunan ruas-ruas garis berarah (masing-masing memiliki panjang dan arah yang sama). Akan tetapi dalam prakteknya, biasanya tidak dibedakan antara suatu vektor dan satu ruas garis berarah representasinya.
Contoh 1: Representasi Vektor: Ruas-ruas Garis Berarah
Misal v merepresentasikan ruas garis berarah dari (0, 0) ke (3, 2), dan misalkan u merepresentasikan ruas garis berarah dari (1, 2) ke (4, 4). Tunjukkan bahwa u dan v ekuivalen.
Pembahasan Misalkan P(0, 0) dan Q(3, 2) menjadi titik pangkal dan titik ujung v, dan misalkan R(1, 2) dan S(4, 4) menjadi titik pangkal dan titik ujung u, seperti yang ditunjukkan Gambar 3. Kita dapat menggunakan Rumus Jarak untuk menentukan panjang PQ dan RS memiliki panjang yang sama.







Kedua segmen tersebut memiliki arah yang sama, karena kedua garis tersebut mengarah ke kanan atas pada garis-garis yang memiliki gradien sama.

dan

Karena ruas garis berarah PQ dan RS memiliki panjang dan arah sama, kita dapat menyimpulkan bahwa kedua vektor tersebut ekuivalen. Yaitu, v dan u ekuivalen.

Analisis Penjumlahan Dan Pengurangan Vektor

Untuk keperluan penghitungan tertentu, kadangkadang sebuah vektor yang terletak dalam bidang koordinat sumbu x dan sumbu y harus diuraikan menjadi komponen-komponen yang saling tegak lurus (sumbu x dan sumbu y). Komponen ini merupakan nilai efektif dalam suatu arah yang diberikan. Cara menguraikan vektor seperti ini disebut analisis. Misalnya, vektor A membentuk sudut αterhadap sumbu x positif, maka komponen vektornya adalah:

Ax = A cos α

Ay = A sin α

Besar (nilai) vektor A dapat diketahui dari persamaan:

Sementara itu, arah vektor ditentukan dengan persamaan:

Penjumlahan Vektor

Penjumlahan dua buah vektor ialah mencari sebuah vektor yang komponen-komponennya adalah jumlah dari kedua komponen-komponen vektor pembentuknya.

Dengan kata lain untuk “menjumlahkan dua buah vektor”adalah “mencari resultan”. Untuk vektor-vektor segaris, misalnya vektor A dan B dalam posisi segaris dengan arah yang sama seperti tampak pada gambar (a) berikut maka resultan (jumlah) vektor dituliskan:

R=A+B

Pada kasus penjumlahan vektor yang lain, seperti yang ditunjukkan gambar (b) diatas terdapat dua vektor yang tidak segaris yang mempunyai titik pangkal sama tetapi dengan arah yang berbeda, sehingga membentuk sudut tertentu. Untuk vektor-vektor yang membentuk sudut á , maka jumlah vektor dapat dilukiskan dengan menggunakan metode

tertentu. Cara ini disebut dengan metode jajaran genjang.

Cara melukiskan jumlah dua buah vektor dengan metode jajaran genjang sebagai berikut:

a. titik tangkap A dan B dibuat berimpit dengan memindahkan titik tangkap A ke titik tangkap B, atau sebaliknya;

b. buat jajaran genjang dengan A dan B sebagai sisi-sisinya;

c. tarik diagonal dari titik tangkap sekutu, maka A + B = R adalah diagonal jajaran genjang.

Metode Jajaran Genjang Untuk Penjumlahan Vektor

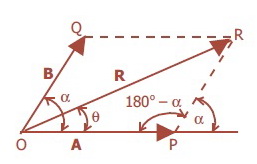
Gambar diatas menunjukkan penjumlahan dua vektor A dan B. Dengan menggunakan persamaan tertentu, dapat diketahui besar dan arah resultan kedua vektor tersebut. Persamaan tersebut diperoleh dengan menerapkan aturan cosinus pada segitiga OPR, sehingga dihasilkan:

(OR)² = (OP)²+ (PR)² – 2 (OP)(PR) cos (180^o– α)

  = (OP)²+ (PR)²– 2 (OP)(PR)(–cos α)

(OR)² = (OP)²+ (PR)²+ 2 (OP)(PR)cos α

Diketahui bahwa OP = A, PR = OQ = B, OR = R, sehingga:

R adalah diagonal panjang jajaran genjang, jika α lancip. Sementara itu, α adalah sudut terkecil yang dibentuk oleh A dan B.

Sebuah vektor mempunyai besar dan arah. Jadi setelah mengetahui besarnya, kita perlu menentukan arah dan resultan vektor tersebut. Arah R dapat ditentukan oleh sudut antara R dan A atau R dan B.

Misalnya sudut θ merupakan sudut yang dibentuk R dan A, maka dengan menggunakan aturan sinus pada segitiga OPR akan diperoleh:

Sehingga :

Dengan menggunakan persamaan tersebut, maka besar sudut θ dapat diketahui.

Metode Segitiga Untuk Penjumlahan Vektor

Metode segitiga merupakan cara lain untuk menjumlahkan dua vektor, selain metode jajaran genjang. Dua buah vektor A dan B, yang pergerakannya ditunjukkan metode segitia (a)diatas, akan mempunyai resultan yang persamaannya dituliskan:

R = A + B

Resultan dua vektor akan diperoleh dengan menempatkan pangkal vektor yang kedua pada ujung vektor pertama. Resultan vektor tersebut diperoleh dengan menghubungkan titik pangkal vektor pertama dengan ujung vektor kedua.

Pada metode segitiga (b)diatas pergerakan dimulai dengan vektor B dilanjutkan dengan A, sehingga diperoleh persamaan:

R = B + A

Jadi,

A + B = B + A

Hasil yang diperoleh ternyata tidak berubah. Jadi, dapat disimpulkan bahwa penjumlahan vektor bersifat komutatif. Tahapan-tahapan penjumlahan vektor dengan metode segitiga adalah sebagai berikut:

a) pindahkan titik tangkap salah satu vektor ke ujung berikutnya,

b) hubungkan titik tangkap vektor pertama ke ujung vektor kedua yang menunjukkan resultan kedua vektor tersebut,

c) besar dan arah R _ dicari dengan aturan cosinus dan sinus.

Jika penjumlahan lebih dari dua buah vektor, maka dijumlahkan dulu dua buah vektor, resultannya dijumlahkan dengan vektor ke-3 dan seterusnya. Misalnya, penjumlahan tiga buah vektor A, B, dan C yang ditunjukkan pada penjumlahan lebih dari 2 vektor berikut.

Penjumlahan 2 Vektor

Pertama-tama kita jumlahkan vektor A dan B yang akan menghasilkan vektor V. Selanjutnya, vektor V tersebut dijumlahkan dengan vektor C sehingga dihasilkan resultan R, yang dituliskan:

R = (A + B) + C = V + C

Cara lain yaitu dengan menjumlahkan vektor B dan C untuk menghasilkan W, yang kemudian dijumlahkan dengan vektor A, sehingga diperoleh resultan R, yaitu:

R = A + (B + C) = A + W

Jika banyak vektor, maka penjumlahan vektor dilakukan dengan menggunakan metode poligon (segi banyak) seperti berikut.

Metode Poligon Untuk Penjumlahan Vektor

Pengurangan Vektor

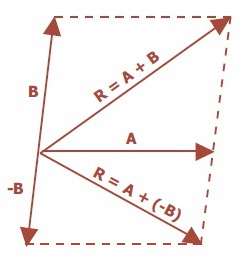
Pengurangan vektor pada prinsipnya sama dengan penjumlahan, tetapi dalam hal ini salah satu vektor mempunyai arah yang berlawanan. Misalnya, vektor A dan B, jika dikurangkan maka:

A – B = A + (-B)

Di mana, –B adalah vektor yang sama dengan B, tetapi berlawanan arah.

Selisih Vektor A-B