BAB IV. KOORDINAT DAN PERSAMAAN KUTUB

BAB : 4 KOORDINAT DAN PERSAMAAN KUTUB

    A.  Sistem koordinat kutub 

       Sistem koordinat kutub dalam suatu bidang terdiri dari satu titik tetap O yang disebut titik asal atau titik kutub dan sebuah garis berarah yang bermula dari titik asal tersebut, yang disebut dengan sumbu kutub. Dalam koordinat kutub, setiap titik P dinyatakan dalam pasangan (r, θ), di mana r adalah jarak titik P ke titik asal, dan θ adalah sudut dari sumbu kutub ke garis OP. Bilangan r disebut koordinat radial dan q disebut koordinat angular atau sudut kutub dari P. Sudut dinyatakan dalam angka positif jika diukur berlawanan jarum jam dan dinyatakan dengan angka negatif jika diukur searah jarum jam.

Beberapa contoh koordinat kutub:

Beberapa koordinat kutub ini menyatakan posisi titik yang sama:

Hubungan antara Koordinat Kutub dan Koordinat Cartesius

Hubungan antara koordinat kutub dan koordinat Cartesius dapat dilihat pada gambar berikut ini:

Untuk menyatakan koordinat Cartesius dalam koordinat kutub dapat digunakan rumus berikut:

Sedangkan untuk menyatakan koordinat kutub dalam koordinat Cartesius dapat digunakan rumus berikut:

Contoh 1:

Contoh 2:

Dapatkan koordinat Cartesius dari (3, –45°)

Jawab:

Sketsa Grafik dalam Koordinat Kutub

Suatu grafik dapat dinyatakan dalam sistem koordinat kutub. Untuk membuat sketsanya, akan lebih mudah jika menggunakan tabel untuk mencari nilai r untuk θ dari 0 hingga 2π radian.

Contoh:

Sketsalah grafik r = 4 sin 2θ

Tabel:

B

   B.  KOORDINAT KUTUB (POLAR)

Dalam sistem koordinat kutub hanya menggunakan sebuah sinar garis sebagai patokan muka. Biasanya sinar garis ini digambar mendatar dan mengarah ke kanan seperti tampak pada gambar 1 sinar garis dinamakan sumbu kutub, sedangkan titik pangkalnya yang biasanya diberi dengan huruf O disebut kutub atau titik asal.

Jika dilihat dari kutub utara didapatkan gambar seperti gambar 2 berikut.

Koordinat kutub dapat dinyatakan sebagai berikut.

Dimisalkan sebuah lingkaran berpusat di O. Kemudian titik A berada pada lingakaran sehingga OA adalah sebuah jari-jari. Antara sumbu kutub dengan jari-jari, akan membentuk sebuah sudut θ. sehingga didapatlah koordinat kutub adalah (r, θ).

Hubungan Koordinat Kutub dan Koordinat Kartesius.

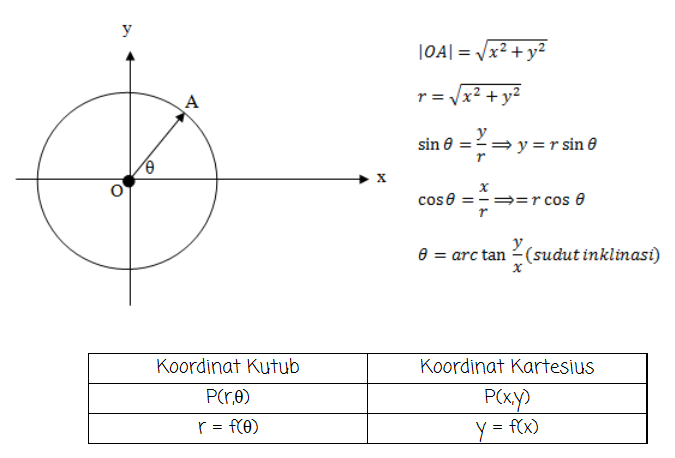
Contoh:

1.

2. 

Diketahui : <xOB = 1350 dan r = 4                                   

Ditanya : Tentukanlah koordinat B pada koordinat kartesius.

Penyelesaian :

x = r cos θ y = r sin θ

x = 4 cos 1350 y = 4 sin 1350

x = 4 (-0,707) y = 4 (0,707)

x = -2,828 y = 2,828

Sehingga koordinat kartesius B adalah (-2,828 ; 2,828)

B.   Persamaan Kutub

Jika fungsi y = x => y – x = 0

y – x = 0

r sin θ – r cos θ = 0

r (sin θ – cos θ) = 0

r ≠ 0 ; (sin θ – cos θ) = 0

sin θ = cos θ

θ = 450

Jika fungsi y + x = 0

y + x = 0

r sin θ + r cos θ = 0

r (sin θ + cos θ) = 0

r ≠ 0 ; (sin θ + cos θ) = 0

sin θ = - cos θ

θ = 1350

θ = 3/4 π rad = -1/4 π rad

Contoh :

Persamaan fungsi dalam koordinat polar dengan jari-jari 6. Tentukanlah persamaan fungsi dalam koordinat kartesius.

Penyelesaian :

Jadi, persamaan fungsi dalam koordinat polar adalah x2 + y2 = 36